Jika 8m = 27, maka 2.4m – 2m+1 = …
A. 12
B. 15
C. 18
D. 21
E. 24
PEMBAHASAN :
8m = 27
(23)m = 33
2m = 3
2.4m – 2m+1 = 2.22m – 2.2m
= 2.(2m)2 – 2.2m
= 2.(3)2 – 2.3
= 18 – 6
= 12
JAWABAN : A
Jika 3log a + 2(3log b) = 1 dan 3log b + 2(3log a) = 2, maka nilai ab adalah …
A. 2
B. 3
C. 6
D. 9
E. 12
PEMBAHASAN :
3log a + 2(3log b) = 1
3log a + 3log b2 = 1
3log ab2 = 1
ab2 = 31
a = 3/b2 … (i)
3log b + 2(3log a) = 2
3log b + 3log a2 = 2
3log a2b = 2
a2b = 32 … (ii)
substitusi pers (i) ke pers (ii), sehingga
(3/b2)2b = 32
(32/b4)b = 32
32/32 = b3
1 = b
a = 3/b2
= 3/12
= 3
maka a.b = 3.1 = 3
JAWABAN : B
Persamaan kuadrat x2 – (a + 1)x + a = 0 mempunyai akar-akar x1 dan x2. Jika x1(x2 – 1) = 3, maka nilai a adalah …
A. 4
B. 3
C. 2
D. -3
E. -4
PEMBAHASAN :
PK : x2 – (a + 1)x + a = 0
x1 + x2 = -b/a = a + 1
x1 . x2 = c/a = a
x1(x2 – 1) = 3
x1x2 – x1 = 3
a – x1 = 3
x1 = a – 3
x1 + x2 = a + 1
(a – 3) + x2 = a + 1
x2 = 4
x1 . x2 = a
x1 = a/4
x1 = a – 3
a/4 = a – 3
a = 4a – 12
a = 3
JAWABAN : B
Jika grafik fungsi kuadrat f(x) = ax2 + bx + c mempunyai titik puncak (8, 4) dan memotong sumbu-x negatif, maka …
A. a > 0, b > 0, dan c > 0
B. a < 0, b < 0, dan c > 0
C. a < 0, b > 0, dan c < 0
D. a > 0, b > 0, dan c < 0
E. a < 0, b > 0, dan c > 0
PEMBAHASAN :
Karena titik puncak berada pada sumbu-y positif dan kurva memotong sumbu-x negatif maka dapat dipastikan membentuk kurva terbuka kebawah sehingga a < 0.
Berdasarkan fakta diatas, dapat diambil kesimpulan bahwa kurva memotong di sumbu-y positif sehingga diperoleh c > 0.
f'(x) = 2ax + b = 0
f'(8) = 16a + b = 0
b = -16a
karena a < 0 dan misal –a = d, diperoleh
b = 16d
jadi b haruslah positif atau b > 0
JAWABAN : E
Ibu mendapatkan potongan harga sebesar 25% dari total pembelian barang di suatu toko. Toko tersebut membebankan pajak sebesar 10% dari harga total pembelian setelah dipotong. Jika x adalah harga total pembelian, maka ibu harus membayar sebesar …
A. (0.1 x 0.25)
B. (0.9 x 0.25)
C. (0.9 x 0.75)
D. (1.1 x 0.25)
E. (1.1 x 0.75)
PEMBAHASAN :
diketahui : harga total pembelian = 
diskon = 25% 
= 0.25 
harga setelah di diskon = harga total pembelian – diskon
=  – 0.25
– 0.25 
= 0.75 
pajak = harga setelah di diskon x 10%
= 10% (0.75  )
)
= 0.1 x 0.75 
harga yang harus dibayar = harga setelah di diskon + pajak
= 0.75  + 0.1 x 0.75
+ 0.1 x 0.75 
= (1 + 0.1) 0.75 
= (1.1 x 0.75) 
JAWABAN : E
Jika 1 < a < 2, maka semua nilai x yang memenuhi pertidaksamaan 
 0 adalah …
0 adalah …
A. x < -3 atau x > 0
B. x < -3 atau x  -2
-2
C. x  -2 atau x
-2 atau x 
D. -3 < x < 0
E. -2  x < 0
x < 0
PEMBAHASAN :
D = b2 – 4ac
= (2a)2 – 4(-1)(-6)
= 4a2 – 24
karena 1 < a < 2, maka 4a2 – 24 < 0
atau D < 0, artinya pembilang tidak memiliki akar2 riil.
x2 + 3x = x(x + 3)
x = 0 atau x = -3
berdasarkan garis bilangan diperoleh -3 < x < 0
JAWABAN : D
Ipin ingin membeli sepeda dengan harga dua kali sepeda yang ingin dibeli Unyil. Unyil telah memiliki Rp 150.000,00 dan akan menabung Rp 3.000,00 per minggu. Ipin telah memiliki Rp 100.000,00 dan akan menabung Rp 10.000 per minggu. Harga sepeda yang akan dibeli Unyil adalah …
A. Rp 200.000,00
B. Rp 300.000,00
C. Rp 400.000,00
D. Rp 500.000,00
E. Rp 600.000,00
PEMBAHASAN :
misal : sepeda Unyil = U dan sepeda Ipin = I
n = jumlah minggu
I = 2U
100.000 + 10.000 n = 2(150.000 + 3.000 n)
100.000 + 10.000 n = 300.000 + 6.000 n
4.000 n = 200.000
n = 50
harga sepeda Unyil = 150.000 + 3.000 n
= 150.000 + 3.000 (50)
= 150.000 + 150.000
= 300.000
JAWABAN : B
Distribusi berat bayi lahir di rumah sakit A dan B dapat dilihat pada diagram berikut.
gambar menyusul
Berat badan bayi dikatakan normal apabila bertanya saat lahir lebih dari 2500 gram. Banyak bayi normal yang lahir di dua rumah sakit tersebut adalah …
A. 12
B. 32
C. 44
D. 128
E. 172
PEMBAHASAN :
diagram pertama (RS A) : 60 dan 32
diagram kedua (RS B) : 68 dan 12
jadi banyak bayi yang lahir normal di dua rumah sakit adalah 60 + 32 + 68 + 12 = 172 bayi
JAWABAN : E
Median, rata-rata dan modus dari data yang terdiri dari atas empat bilangan asli adalah 7. Jika selisih antara data terbesar dan data terkecil adalah 6, maka hasil kali empat data tersebut adalah …
 =
= 
A. 1864
B. 1932
C. 1960
D. 1976
E. 1983
PEMBAHASAN :
Diket : Me = Mo =  = 7
= 7
misal 4 bilangan yang dimaksud adalah a, b, c dan d (sudah terurut).
d – a = 6  a = d – 6
a = d – 6
Me =  = 7
= 7
b + c = 14
7 = 
28 = 2d + 8
10 = d
sehingga diperoleh a = 4
karena Mo = 7 dan b + c = 14, maka b = c = 7
jadi a.b.c.d = 4.7.7.10 = 1960
JAWABAN : C
Jika  , maka nilai a yang memenuhi
, maka nilai a yang memenuhi  = -5 adalah …
= -5 adalah …


 =
= 
 =
= 
A. 1
B. 1/2
C. -1
D. -3/2
E. -2
PEMBAHASAN :
= 
-5 = 
-5(a + 2) = 2a – 3
-5a – 10 = 2a – 3
7a = -7
a = -1
JAWABAN : C
Jika A =  , B =
, B =  dan AB =
dan AB =  , maka nilai a + c adalah …
, maka nilai a + c adalah …
 =
= 
A. 0
B. 1
C. 2
D. 5
E. 9
PEMBAHASAN :
AB = 

kolom 1 baris 1 : 3 = 2a – b + 4c
kolom 2 baris 1 : 1 = 2a + b
b = 1 – 2a
3 = 2a – (1 – 2a) + 4c
3 = 4a + 4c – 1
4 = 4a + 4c
1 = a + c
JAWABAN : B
Diketahui a, b, dan c berturut-turut adalah suku ke-2, ke-4, dan ke-6 suatu barisan aritmatika. Jika  = 4, maka nilai b adalah …
= 4, maka nilai b adalah …
 = 4
= 4
 = 4
= 4
 = 4
= 4
A. -4
B. -2
C. 1
D. 2
E. 4
PEMBAHASAN :
misal : suku awal := x dan beda := y
Un = x + (n – 1)y
U2 = x + y = a
U4 = x + 3y = b
U6 = x + 5y = c
3x + 9y = 4x + 12y + 4
x + 3y = -4
b = -4
JAWABAN : A
Diketahui deret geometri tak hingga u1 + u2 + u3 + … . Jika rasio deret tersebut adalah r dengan -1 < r < 1, u2 + u4 + u6 + … = 4, dan u2+ u4 = 15/4, maka nilai r adalah …
 = 4
= 4
A.  atau
atau 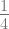
B.  atau
atau 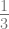
C.  atau
atau 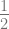
D.  atau
atau 
E.  atau
atau 
PEMBAHASAN :
NOTE : Sganjil = 
Sgenap = 
u2 + u4 + u6 + … = 4
ar = 4(1 – r2) … (i)
u2 + u4 = 15/4
ar + ar3 = 15/4
ar(1 + r2) = 15/4 … (ii)
substitusi per (i) ke pers (ii),
4(1 – r2)(1 + r2) = 15/4
16(1 – r4) = 15
16 – 16r4 = 15
16r4 = 1
r4 = 1/16
r21,2 = 1/4 atau r23,4 = -1/4
r1 = 1/2 atau r2 = -1/2 (r23,4 = -1/4 [hasilnya imajiner])
JAWABAN : C
Parabola y = x2 – (k + 2)x + 2k memotong sumbu-y di (0, c) dan memotong sumbu-x di (a, 0) dan (b, 0). Jika a + 2, c, dan a + 2b membentuk barisan aritmatika, maka nilai k adalah …
A. 3
B. 2
C. 1
D. 1/3
E. -1/3
PEMBAHASAN :
titik (0, c)
c = (0)2 – (k + 2)(0) + 2k
c = 2k
titik potong
x1,2 = 
= 
= 
= 
= 
= 
x1 = [(k + 2) + (k – 2) = k
x2 = [(k + 2) – (k – 2) = 2
karena parabola memotong sumbu-x di (a, 0) dan (b, 0) maka x1 = a = katau x2 = b = 2
barisan aritmatika : a + 2, c, dan a + 2b
c – (a + 2) = (a + 2b) – c
2c = (a + 2b) + (a + 2)
2c = 2a + 2b + 2
c = a + b + 1
2k = k + 2 + 1
k = 3
JAWABAN : A
Kode kupon hadiah untuk belanja pada suatu toko swalayan berbentuk bilangan yang disusun dari angka 1, 3, 3, 6, 9. Jika kupon-kupon tersebut disusun berdasarkan kodenya mulai dari yang terkecil sampai dengan yang terbesar, maka kupon dengan kode kurang dari 63000 sebanyak …
A. 51
B. 40
C. 39
D. 36
E. 24
PEMBAHASAN :

